lets draw 3d shapes together
d3-shape
Visualizations typically consist of discrete graphical marks, such equally symbols, arcs, lines and areas. While the rectangles of a bar chart may exist easy enough to generate straight using SVG or Canvas, other shapes are circuitous, such as rounded annular sectors and centripetal Catmull–Rom splines. This module provides a variety of shape generators for your convenience.
Every bit with other aspects of D3, these shapes are driven by data: each shape generator exposes accessors that control how the input data are mapped to a visual representation. For case, y'all might define a line generator for a time series past scaling fields of your data to fit the chart:
const line = d3 . line ( ) . x ( d => x ( d . date ) ) . y ( d => y ( d . value ) ) ; This line generator tin and then be used to compute the d aspect of an SVG path element:
path . datum ( data ) . attr ( "d" , line ) ; Or you can use it to return to a Sheet 2nd context:
line . context ( context ) ( data ) ; For more than, read Introducing d3-shape.
Installing
If you use npm, npm install d3-shape. You can too download the latest release on GitHub. For vanilla HTML in modern browsers, import d3-shape from Skypack:
< script blazon="module"> import { line } from "https://cdn.skypack.dev/d3-shape@iii" ; const l = line ( ) ; </ script >
For legacy environments, you can load d3-shape'due south UMD bundle from an npm-based CDN such as jsDelivr; a d3 global is exported:
< script src="https://cdn.jsdelivr.net/npm/d3-path@3"> </ script > < script src="https://cdn.jsdelivr.internet/npm/d3-shape@3"> </ script > < script > const l = d3 . line ( ) ; </ script > API Reference
- Arcs
- Pies
- Lines
- Areas
- Curves
- Custom Curves
- Links
- Symbols
- Custom Symbol Types
- Stacks
Note: all the methods that accept arrays also accept iterables and convert them to arrays internally.
Arcs
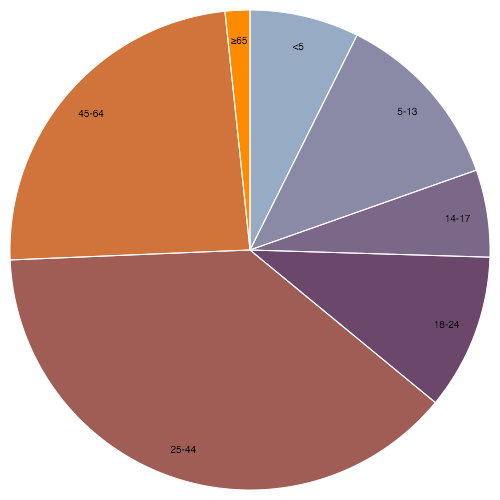
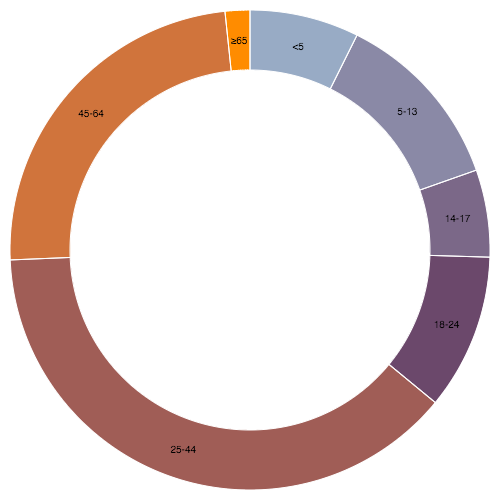
The arc generator produces a round or annular sector, every bit in a pie or donut nautical chart. If the accented difference betwixt the starting time and end angles (the angular span) is greater than τ, the arc generator will produce a complete circumvolve or annulus. If information technology is less than τ, the arc'south angular length will be equal to the absolute deviation between the two angles (going clockwise if the signed difference is positive and anticlockwise if it is negative). If the accented deviation is less than τ, the arc may have rounded corners and angular padding. Arcs are always centered at ⟨0,0⟩; use a transform (encounter: SVG, Canvas) to movement the arc to a unlike position.
See also the pie generator, which computes the necessary angles to stand for an array of data every bit a pie or donut chart; these angles tin then exist passed to an arc generator.
# d3.arc() · Source
Constructs a new arc generator with the default settings.
# arc(arguments…) · Source
Generates an arc for the given arguments. The arguments are arbitrary; they are simply propagated to the arc generator's accessor functions along with the this object. For example, with the default settings, an object with radii and angles is expected:
const arc = d3 . arc ( ) ; arc ( { innerRadius: 0 , outerRadius: 100 , startAngle: 0 , endAngle: Math . PI / two } ) ; // "M0,-100A100,100,0,0,1,100,0L0,0Z" If the radii and angles are instead defined as constants, you can generate an arc without whatever arguments:
const arc = d3 . arc ( ) . innerRadius ( 0 ) . outerRadius ( 100 ) . startAngle ( 0 ) . endAngle ( Math . PI / 2 ) ; arc ( ) ; // "M0,-100A100,100,0,0,1,100,0L0,0Z" If the arc generator has a context, and then the arc is rendered to this context every bit a sequence of path method calls and this role returns void. Otherwise, a path data string is returned.
# arc.centroid(arguments…) · Source
Computes the midpoint [x, y] of the center line of the arc that would be generated past the given arguments. The arguments are arbitrary; they are simply propagated to the arc generator's accessor functions along with the this object. To exist consequent with the generated arc, the accessors must exist deterministic, i.e., return the aforementioned value given the same arguments. The midpoint is divers as (startAngle + endAngle) / two and (innerRadius + outerRadius) / 2. For example:
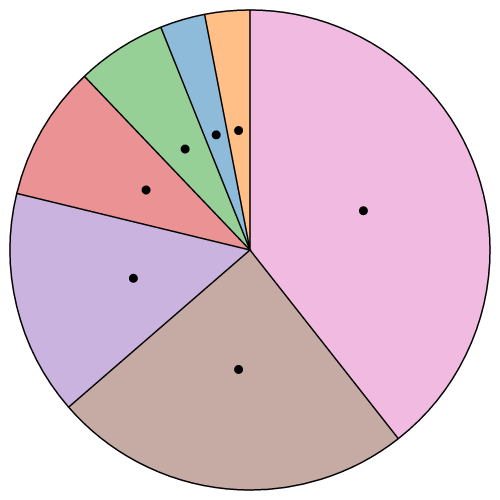
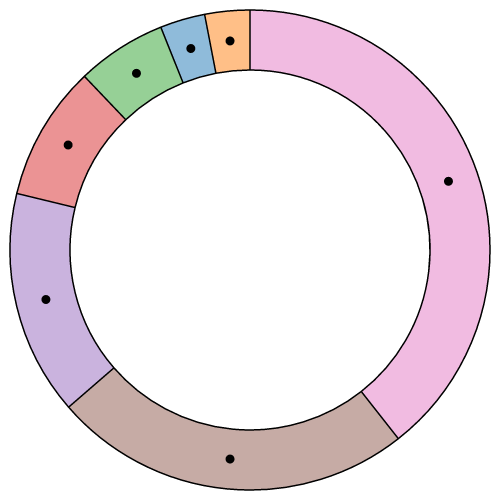
Note that this is not the geometric centre of the arc, which may exist outside the arc; this method is merely a convenience for positioning labels.
# arc.innerRadius([radius]) · Source
If radius is specified, sets the inner radius to the specified part or number and returns this arc generator. If radius is not specified, returns the current inner radius accessor, which defaults to:
function innerRadius ( d ) { return d . innerRadius ; } Specifying the inner radius as a function is useful for constructing a stacked polar bar chart, often in conjunction with a sqrt calibration. More than ordinarily, a constant inner radius is used for a donut or pie chart. If the outer radius is smaller than the inner radius, the inner and outer radii are swapped. A negative value is treated as zero.
# arc.outerRadius([radius]) · Source
If radius is specified, sets the outer radius to the specified role or number and returns this arc generator. If radius is not specified, returns the current outer radius accessor, which defaults to:
function outerRadius ( d ) { return d . outerRadius ; } Specifying the outer radius as a part is useful for constructing a coxcomb or polar bar nautical chart, often in conjunction with a sqrt scale. More commonly, a abiding outer radius is used for a pie or donut nautical chart. If the outer radius is smaller than the inner radius, the inner and outer radii are swapped. A negative value is treated as zero.
# arc.cornerRadius([radius]) · Source
If radius is specified, sets the corner radius to the specified part or number and returns this arc generator. If radius is not specified, returns the electric current corner radius accessor, which defaults to:
function cornerRadius ( ) { render 0 ; } If the corner radius is greater than nada, the corners of the arc are rounded using circles of the given radius. For a circular sector, the 2 outer corners are rounded; for an annular sector, all four corners are rounded. The corner circles are shown in this diagram:
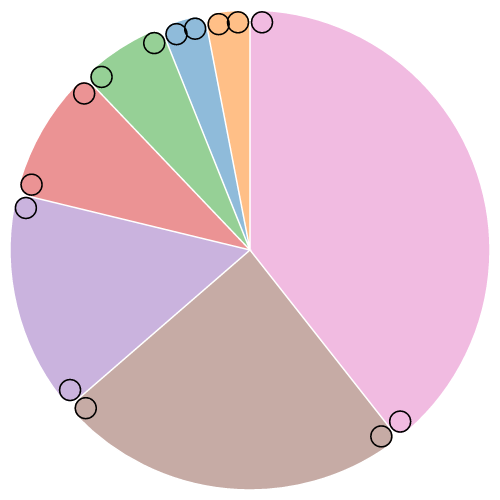
The corner radius may not be larger than (outerRadius - innerRadius) / ii. In improver, for arcs whose angular span is less than π, the corner radius may exist reduced as two next rounded corners intersect. This is occurs more than often with the inner corners. See the arc corners animation for illustration.
# arc.startAngle([bending]) · Source
If angle is specified, sets the beginning bending to the specified office or number and returns this arc generator. If angle is non specified, returns the electric current start angle accessor, which defaults to:
office startAngle ( d ) { return d . startAngle ; } The angle is specified in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise. If |endAngle - startAngle| ≥ τ, a complete circle or annulus is generated rather than a sector.
# arc.endAngle([bending]) · Source
If angle is specified, sets the end bending to the specified office or number and returns this arc generator. If angle is not specified, returns the current end angle accessor, which defaults to:
function endAngle ( d ) { return d . endAngle ; } The angle is specified in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise. If |endAngle - startAngle| ≥ τ, a complete circle or annulus is generated rather than a sector.
# arc.padAngle([angle]) · Source
If bending is specified, sets the pad angle to the specified role or number and returns this arc generator. If angle is not specified, returns the current pad angle accessor, which defaults to:
function padAngle ( ) { return d && d . padAngle ; } The pad angle is converted to a fixed linear distance separating adjacent arcs, divers equally padRadius * padAngle. This distance is subtracted equally from the start and end of the arc. If the arc forms a complete circle or annulus, as when |endAngle - startAngle| ≥ τ, the pad angle is ignored.
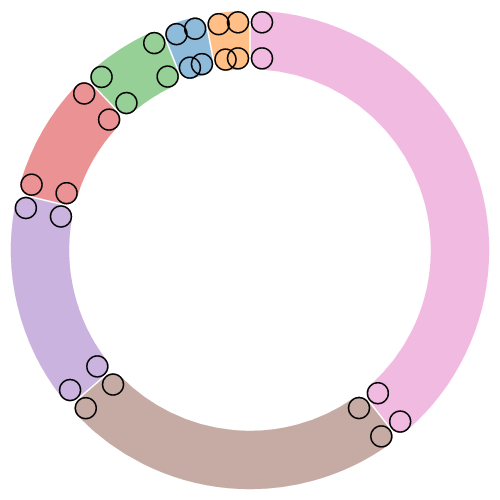
If the inner radius or angular span is small relative to the pad angle, information technology may not be possible to maintain parallel edges betwixt adjacent arcs. In this case, the inner edge of the arc may plummet to a point, like to a round sector. For this reason, padding is typically merely practical to annular sectors (i.e., when innerRadius is positive), equally shown in this diagram:
The recommended minimum inner radius when using padding is outerRadius * padAngle / sin(θ), where θ is the athwart span of the smallest arc before padding. For example, if the outer radius is 200 pixels and the pad angle is 0.02 radians, a reasonable θ is 0.04 radians, and a reasonable inner radius is 100 pixels. Encounter the arc padding animation for illustration.
Often, the pad angle is non set directly on the arc generator, but is instead computed by the pie generator so every bit to ensure that the expanse of padded arcs is proportional to their value; encounter pie.padAngle. See the pie padding animation for analogy. If you employ a constant pad angle to the arc generator directly, it tends to subtract unduly from smaller arcs, introducing distortion.
# arc.padRadius([radius]) · Source
If radius is specified, sets the pad radius to the specified part or number and returns this arc generator. If radius is non specified, returns the current pad radius accessor, which defaults to null, indicating that the pad radius should be automatically computed every bit sqrt(innerRadius * innerRadius + outerRadius * outerRadius). The pad radius determines the fixed linear distance separating adjacent arcs, divers as padRadius * padAngle.
# arc.context([context]) · Source
If context is specified, sets the context and returns this arc generator. If context is not specified, returns the current context, which defaults to zilch. If the context is not cipher, then the generated arc is rendered to this context as a sequence of path method calls. Otherwise, a path information string representing the generated arc is returned.
Pies
The pie generator does not produce a shape directly, but instead computes the necessary angles to represent a tabular dataset every bit a pie or donut chart; these angles can then be passed to an arc generator.
# d3.pie() · Source
Constructs a new pie generator with the default settings.
# pie(data[, arguments…]) · Source
Generates a pie for the given array of data, returning an array of objects representing each datum'south arc angles. Any additional arguments are arbitrary; they are only propagated to the pie generator'due south accessor functions along with the this object. The length of the returned assortment is the same as data, and each element i in the returned array corresponds to the chemical element i in the input data. Each object in the returned array has the following backdrop:
-
information- the input datum; the corresponding element in the input data array. -
value- the numeric value of the arc. -
index- the aught-based sorted index of the arc. -
startAngle- the start angle of the arc. -
endAngle- the end angle of the arc. -
padAngle- the pad angle of the arc.
This representation is designed to work with the arc generator'southward default startAngle, endAngle and padAngle accessors. The angular units are arbitrary, but if you plan to utilize the pie generator in conjunction with an arc generator, you should specify angles in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise.
Given a small dataset of numbers, here is how to compute the arc angles to render this data as a pie chart:
const data = [ i , 1 , 2 , iii , 5 , viii , 13 , 21 ] ; const arcs = d3 . pie ( ) ( data ) ; The first pair of parens, pie(), constructs a default pie generator. The second, pie()(data), invokes this generator on the dataset, returning an array of objects:
[ {"information": 1, "value": 1, "index": half-dozen, "startAngle": six.050474740247008, "endAngle": 6.166830023713296, "padAngle": 0}, {"information": i, "value": ane, "index": 7, "startAngle": 6.166830023713296, "endAngle": half dozen.283185307179584, "padAngle": 0}, {"data": 2, "value": 2, "alphabetize": 5, "startAngle": 5.817764173314431, "endAngle": 6.050474740247008, "padAngle": 0}, {"information": iii, "value": 3, "index": 4, "startAngle": 5.468698322915565, "endAngle": five.817764173314431, "padAngle": 0}, {"data": five, "value": 5, "alphabetize": three, "startAngle": 4.886921905584122, "endAngle": 5.468698322915565, "padAngle": 0}, {"data": eight, "value": viii, "index": 2, "startAngle": 3.956079637853813, "endAngle": 4.886921905584122, "padAngle": 0}, {"data": thirteen, "value": thirteen, "index": 1, "startAngle": 2.443460952792061, "endAngle": 3.956079637853813, "padAngle": 0}, {"data": 21, "value": 21, "index": 0, "startAngle": 0.000000000000000, "endAngle": two.443460952792061, "padAngle": 0} ] Annotation that the returned assortment is in the aforementioned order equally the data, even though this pie chart is sorted by descending value, starting with the arc for the concluding datum (value 21) at 12 o'clock.
# pie.value([value]) · Source
If value is specified, sets the value accessor to the specified function or number and returns this pie generator. If value is not specified, returns the current value accessor, which defaults to:
office value ( d ) { return d ; } When a pie is generated, the value accessor will be invoked for each element in the input information array, being passed the element d, the index i, and the assortment data as three arguments. The default value accessor assumes that the input data are numbers, or that they are coercible to numbers using valueOf. If your data are non simply numbers, then yous should specify an accessor that returns the corresponding numeric value for a given datum. For example:
const information = [ { "number": 4 , "name": "Locke" } , { "number": 8 , "proper name": "Reyes" } , { "number": fifteen , "name": "Ford" } , { "number": 16 , "name": "Jarrah" } , { "number": 23 , "name": "Shephard" } , { "number": 42 , "proper noun": "Kwon" } ] ; const arcs = d3 . pie ( ) . value ( d => d . number ) ( information ) ; This is similar to mapping your data to values before invoking the pie generator:
const arcs = d3 . pie ( ) ( data . map ( d => d . number ) ) ; The benefit of an accessor is that the input data remains associated with the returned objects, thereby making it easier to access other fields of the data, for example to fix the color or to add together text labels.
# pie.sort([compare]) · Source
If compare is specified, sets the information comparator to the specified function and returns this pie generator. If compare is non specified, returns the current data comparator, which defaults to zilch. If both the information comparator and the value comparator are nix, so arcs are positioned in the original input order. Otherwise, the data is sorted according to the data comparator, and the resulting lodge is used. Setting the data comparator implicitly sets the value comparator to null.
The compare part takes two arguments a and b, each elements from the input data array. If the arc for a should be earlier the arc for b, so the comparator must render a number less than zero; if the arc for a should be after the arc for b, then the comparator must return a number greater than zero; returning cypher means that the relative order of a and b is unspecified. For example, to sort arcs by their associated name:
pie . sort ( ( a , b ) => a . proper noun . localeCompare ( b . proper noun ) ) ; Sorting does not touch on the club of the generated arc array which is always in the aforementioned order as the input data array; it just affects the computed angles of each arc. The first arc starts at the start angle and the concluding arc ends at the end angle.
# pie.sortValues([compare]) · Source
If compare is specified, sets the value comparator to the specified role and returns this pie generator. If compare is not specified, returns the current value comparator, which defaults to descending value. The default value comparator is implemented as:
office compare ( a , b ) { return b - a ; } If both the data comparator and the value comparator are null, then arcs are positioned in the original input order. Otherwise, the data is sorted according to the data comparator, and the resulting order is used. Setting the value comparator implicitly sets the data comparator to goose egg.
The value comparator is similar to the data comparator, except the two arguments a and b are values derived from the input data array using the value accessor, not the data elements. If the arc for a should exist before the arc for b, then the comparator must render a number less than zero; if the arc for a should be after the arc for b, then the comparator must return a number greater than zero; returning zero means that the relative order of a and b is unspecified. For example, to sort arcs by ascending value:
pie . sortValues ( ( a , b ) => a - b ) ; Sorting does not bear on the guild of the generated arc array which is ever in the same order as the input data array; information technology simply affects the computed angles of each arc. The kickoff arc starts at the get-go angle and the last arc ends at the stop angle.
# pie.startAngle([angle]) · Source
If angle is specified, sets the overall first angle of the pie to the specified part or number and returns this pie generator. If angle is non specified, returns the current showtime bending accessor, which defaults to:
role startAngle ( ) { return 0 ; } The outset angle hither means the overall start angle of the pie, i.due east., the start angle of the first arc. The beginning bending accessor is invoked once, being passed the same arguments and this context equally the pie generator. The units of angle are capricious, just if yous plan to use the pie generator in conjunction with an arc generator, yous should specify an angle in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise.
# pie.endAngle([bending]) · Source
If angle is specified, sets the overall end angle of the pie to the specified function or number and returns this pie generator. If angle is not specified, returns the current end angle accessor, which defaults to:
function endAngle ( ) { return 2 * Math . PI ; } The cease angle hither ways the overall cease angle of the pie, i.e., the stop angle of the terminal arc. The stop angle accessor is invoked once, being passed the aforementioned arguments and this context as the pie generator. The units of angle are arbitrary, simply if you plan to apply the pie generator in conjunction with an arc generator, you should specify an angle in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise.
The value of the end angle is constrained to startAngle ± τ, such that |endAngle - startAngle| ≤ τ.
# pie.padAngle([bending]) · Source
If angle is specified, sets the pad bending to the specified function or number and returns this pie generator. If angle is not specified, returns the current pad angle accessor, which defaults to:
function padAngle ( ) { render 0 ; } The pad angle here ways the angular separation between each adjacent arc. The total amount of padding reserved is the specified angle times the number of elements in the input data array, and at most |endAngle - startAngle|; the remaining space is then divided proportionally past value such that the relative area of each arc is preserved. See the pie padding blitheness for illustration. The pad angle accessor is invoked once, being passed the aforementioned arguments and this context as the pie generator. The units of angle are arbitrary, but if yous plan to employ the pie generator in conjunction with an arc generator, yous should specify an angle in radians.
Lines
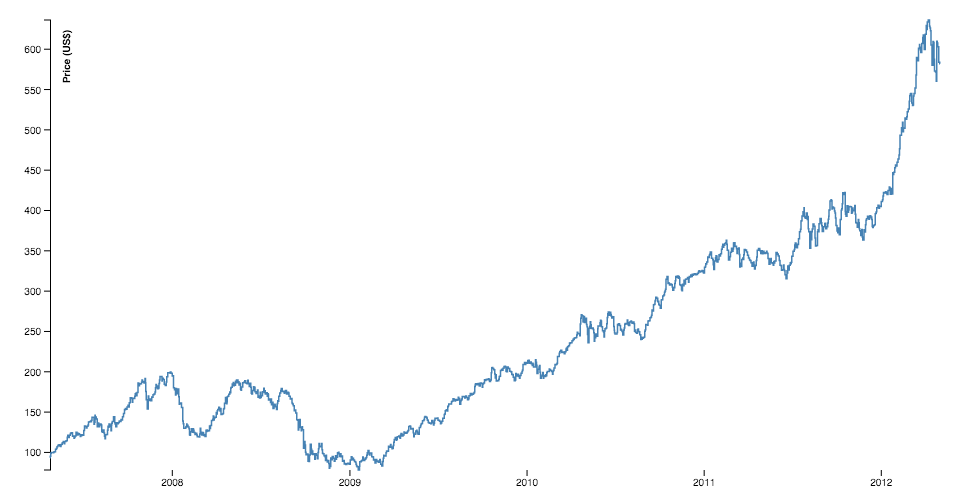
The line generator produces a spline or polyline, as in a line chart. Lines also appear in many other visualization types, such as the links in hierarchical edge bundling.
# d3.line([x][, y]) · Source, Examples
Constructs a new line generator with the default settings. If x or y are specified, sets the corresponding accessors to the specified part or number and returns this line generator.
# line(data) · Source, Examples
Generates a line for the given assortment of data. Depending on this line generator's associated curve, the given input information may need to be sorted by 10-value earlier being passed to the line generator. If the line generator has a context, and then the line is rendered to this context as a sequence of path method calls and this function returns void. Otherwise, a path information string is returned.
# line.x([10]) · Source, Examples
If ten is specified, sets the ten accessor to the specified function or number and returns this line generator. If 10 is not specified, returns the current ten accessor, which defaults to:
office x ( d ) { render d [ 0 ] ; } When a line is generated, the x accessor will be invoked for each defined chemical element in the input data array, being passed the element d, the alphabetize i, and the assortment data as three arguments. The default x accessor assumes that the input information are two-element arrays of numbers. If your data are in a different format, or if you wish to transform the information before rendering, then you should specify a custom accessor. For example, if x is a time scale and y is a linear scale:
const data = [ { date: new Date ( 2007 , 3 , 24 ) , value: 93.24 } , { date: new Date ( 2007 , 3 , 25 ) , value: 95.35 } , { date: new Date ( 2007 , 3 , 26 ) , value: 98.84 } , { date: new Date ( 2007 , 3 , 27 ) , value: 99.92 } , { date: new Date ( 2007 , iii , thirty ) , value: 99.80 } , { engagement: new Engagement ( 2007 , four , i ) , value: 99.47 } , … ] ; const line = d3 . line ( ) . ten ( d => x ( d . engagement ) ) . y ( d => y ( d . value ) ) ; # line.y([y]) · Source, Examples
If y is specified, sets the y accessor to the specified part or number and returns this line generator. If y is not specified, returns the electric current y accessor, which defaults to:
role y ( d ) { render d [ i ] ; } When a line is generated, the y accessor will be invoked for each defined element in the input information assortment, being passed the element d, the index i, and the assortment data as 3 arguments. The default y accessor assumes that the input data are 2-chemical element arrays of numbers. Come across line.x for more than information.
# line.defined([defined]) · Source, Examples
If defined is specified, sets the divers accessor to the specified function or boolean and returns this line generator. If defined is not specified, returns the current defined accessor, which defaults to:
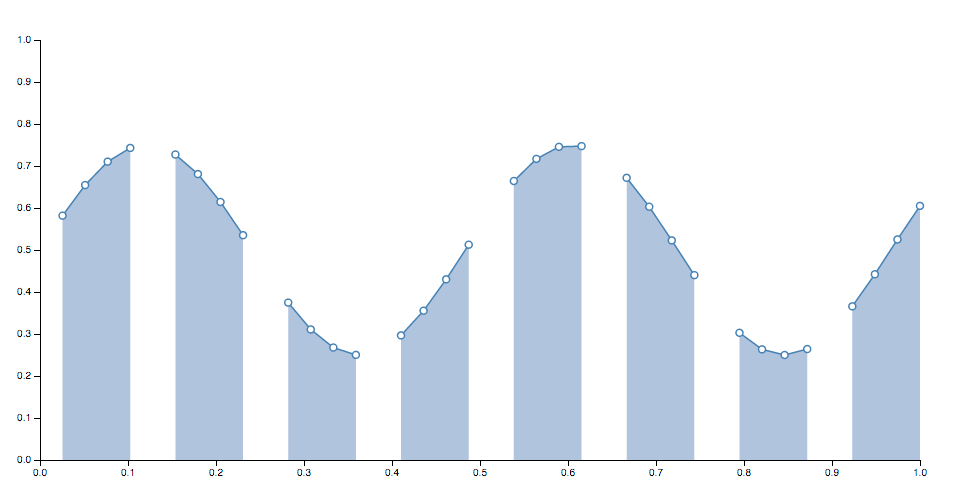
role defined ( ) { return true ; } The default accessor thus assumes that the input data is always divers. When a line is generated, the defined accessor will be invoked for each chemical element in the input data array, being passed the element d, the alphabetize i, and the array data as 3 arguments. If the given chemical element is defined (i.east., if the defined accessor returns a truthy value for this element), the x and y accessors will later exist evaluated and the point will be added to the current line segment. Otherwise, the element will exist skipped, the current line segment will exist ended, and a new line segment will be generated for the next defined signal. Every bit a result, the generated line may have several discrete segments. For instance:
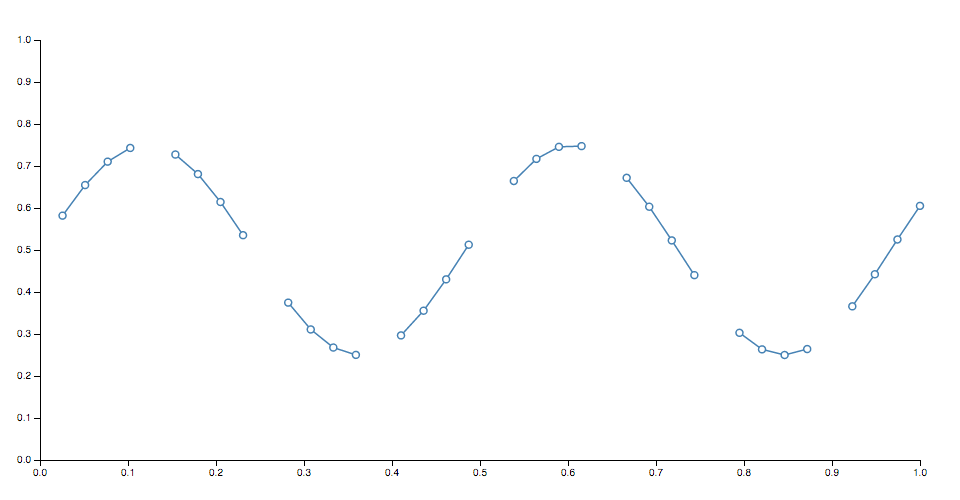
Note that if a line segment consists of merely a single bespeak, it may appear invisible unless rendered with rounded or square line caps. In addition, some curves such as curveCardinalOpen only render a visible segment if it contains multiple points.
# line.bend([curve]) · Source, Examples
If curve is specified, sets the bend mill and returns this line generator. If curve is non specified, returns the electric current curve factory, which defaults to curveLinear.
# line.context([context]) · Source, Examples
If context is specified, sets the context and returns this line generator. If context is not specified, returns the electric current context, which defaults to nil. If the context is not goose egg, then the generated line is rendered to this context as a sequence of path method calls. Otherwise, a path data cord representing the generated line is returned.
# d3.lineRadial() · Source, Examples

Constructs a new radial line generator with the default settings. A radial line generator is equivalent to the standard Cartesian line generator, except the x and y accessors are replaced with angle and radius accessors. Radial lines are always positioned relative to ⟨0,0⟩; apply a transform (see: SVG, Canvas) to alter the origin.
# lineRadial(data) · Source, Examples
Equivalent to line.
# lineRadial.angle([bending]) · Source, Examples
Equivalent to line.x, except the accessor returns the bending in radians, with 0 at -y (12 o'clock).
# lineRadial.radius([radius]) · Source, Examples
Equivalent to line.y, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
# lineRadial.defined([divers])
Equivalent to line.defined.
# lineRadial.curve([curve]) · Source, Examples
Equivalent to line.bend. Notation that curveMonotoneX or curveMonotoneY are not recommended for radial lines because they presume that the information is monotonic in x or y, which is typically untrue of radial lines.
# lineRadial.context([context])
Equivalent to line.context.
Areas
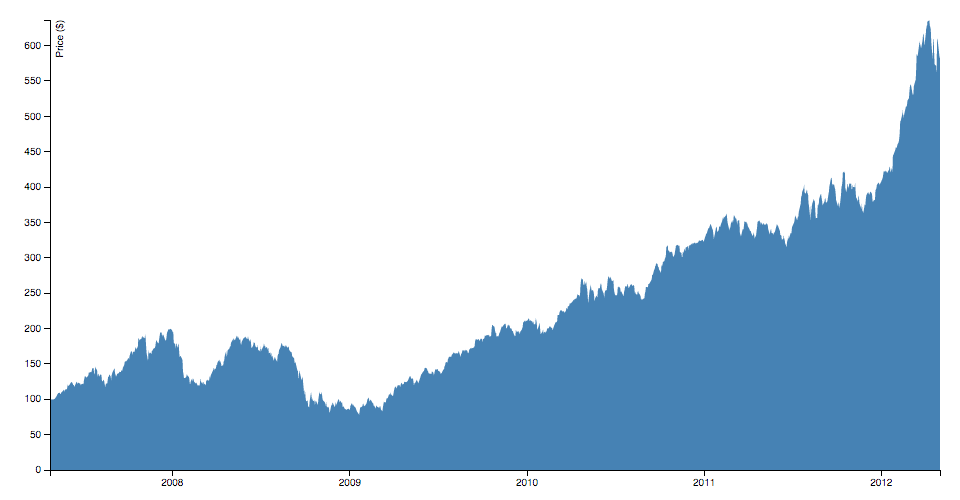
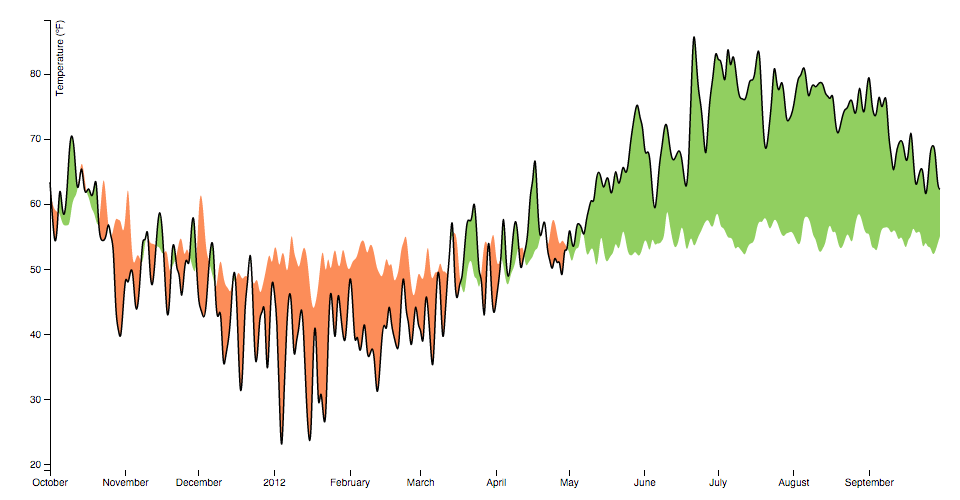
The surface area generator produces an area, every bit in an area chart. An area is defined by two bounding lines, either splines or polylines. Typically, the two lines share the same ten-values (x0 = x1), differing only in y-value (y0 and y1); most normally, y0 is defined as a constant representing nix. The showtime line (the topline) is defined past x1 and y1 and is rendered first; the 2d line (the baseline) is divers by x0 and y0 and is rendered second, with the points in opposite order. With a curveLinear curve, this produces a clockwise polygon.
# d3.area([x][, y0][, y1]) · Source
Constructs a new area generator with the default settings. If x, y0 or y1 are specified, sets the corresponding accessors to the specified function or number and returns this area generator.
# area(data) · Source
Generates an area for the given array of data. Depending on this area generator'south associated curve, the given input data may need to be sorted by x-value before being passed to the area generator. If the area generator has a context, then the area is rendered to this context as a sequence of path method calls and this function returns void. Otherwise, a path data string is returned.
# expanse.ten([ten]) · Source
If ten is specified, sets x0 to x and x1 to null and returns this area generator. If x is not specified, returns the electric current x0 accessor.
# surface area.x0([x]) · Source
If x is specified, sets the x0 accessor to the specified function or number and returns this area generator. If x is not specified, returns the electric current x0 accessor, which defaults to:
office x ( d ) { return d [ 0 ] ; } When an area is generated, the x0 accessor volition be invoked for each divers element in the input data array, being passed the chemical element d, the index i, and the assortment data as three arguments. The default x0 accessor assumes that the input data are two-element arrays of numbers. If your data are in a different format, or if you wish to transform the information before rendering, then you lot should specify a custom accessor. For case, if ten is a time calibration and y is a linear calibration:
const information = [ { date: new Date ( 2007 , 3 , 24 ) , value: 93.24 } , { date: new Engagement ( 2007 , three , 25 ) , value: 95.35 } , { date: new Engagement ( 2007 , iii , 26 ) , value: 98.84 } , { engagement: new Engagement ( 2007 , 3 , 27 ) , value: 99.92 } , { date: new Appointment ( 2007 , three , thirty ) , value: 99.lxxx } , { date: new Date ( 2007 , 4 , ane ) , value: 99.47 } , … ] ; const area = d3 . area ( ) . ten ( d => x ( d . date ) ) . y1 ( d => y ( d . value ) ) . y0 ( y ( 0 ) ) ; # area.x1([x]) · Source
If x is specified, sets the x1 accessor to the specified function or number and returns this area generator. If 10 is not specified, returns the current x1 accessor, which defaults to null, indicating that the previously-computed x0 value should exist reused for the x1 value.
When an area is generated, the x1 accessor will exist invoked for each defined element in the input data array, beingness passed the element d, the alphabetize i, and the array data as three arguments. See expanse.x0 for more information.
# area.y([y]) · Source
If y is specified, sets y0 to y and y1 to null and returns this area generator. If y is not specified, returns the current y0 accessor.
# area.y0([y]) · Source
If y is specified, sets the y0 accessor to the specified function or number and returns this area generator. If y is not specified, returns the electric current y0 accessor, which defaults to:
function y ( ) { return 0 ; } When an expanse is generated, the y0 accessor will be invoked for each defined element in the input data array, existence passed the element d, the alphabetize i, and the assortment information as 3 arguments. See surface area.x0 for more information.
# area.y1([y]) · Source
If y is specified, sets the y1 accessor to the specified role or number and returns this area generator. If y is not specified, returns the current y1 accessor, which defaults to:
function y ( d ) { return d [ 1 ] ; } A null accessor is also immune, indicating that the previously-computed y0 value should be reused for the y1 value. When an area is generated, the y1 accessor volition exist invoked for each divers element in the input data array, being passed the element d, the index i, and the array data as three arguments. See area.x0 for more than information.
# area.divers([defined]) · Source
If defined is specified, sets the divers accessor to the specified function or boolean and returns this expanse generator. If defined is not specified, returns the current defined accessor, which defaults to:
function defined ( ) { return true ; } The default accessor thus assumes that the input data is ever defined. When an area is generated, the defined accessor will be invoked for each element in the input data array, being passed the chemical element d, the index i, and the array information as three arguments. If the given chemical element is defined (i.e., if the defined accessor returns a truthy value for this element), the x0, x1, y0 and y1 accessors will subsequently be evaluated and the point volition be added to the current area segment. Otherwise, the chemical element will be skipped, the electric current area segment will be ended, and a new expanse segment volition be generated for the next defined point. Every bit a consequence, the generated area may accept several discrete segments. For instance:
Note that if an area segment consists of only a single betoken, it may appear invisible unless rendered with rounded or square line caps. In addition, some curves such as curveCardinalOpen simply render a visible segment if information technology contains multiple points.
# area.curve([curve]) · Source
If curve is specified, sets the curve factory and returns this area generator. If curve is non specified, returns the current curve factory, which defaults to curveLinear.
# area.context([context]) · Source
If context is specified, sets the context and returns this area generator. If context is not specified, returns the electric current context, which defaults to null. If the context is not zilch, and then the generated expanse is rendered to this context as a sequence of path method calls. Otherwise, a path data string representing the generated area is returned.
# area.lineX0() · Source
# area.lineY0() · Source
Returns a new line generator that has this area generator'due south current defined accessor, bend and context. The line'due south ten-accessor is this expanse'due south x0-accessor, and the line's y-accessor is this surface area's y0-accessor.
# area.lineX1() · Source
Returns a new line generator that has this surface area generator's current defined accessor, curve and context. The line'south x-accessor is this area'southward x1-accessor, and the line's y-accessor is this area'southward y0-accessor.
# area.lineY1() · Source
Returns a new line generator that has this area generator's current defined accessor, curve and context. The line's 10-accessor is this surface area'due south x0-accessor, and the line'due south y-accessor is this expanse's y1-accessor.
# d3.areaRadial() · Source

Constructs a new radial expanse generator with the default settings. A radial area generator is equivalent to the standard Cartesian area generator, except the x and y accessors are replaced with angle and radius accessors. Radial areas are ever positioned relative to ⟨0,0⟩; employ a transform (run into: SVG, Sheet) to change the origin.
# areaRadial(information)
Equivalent to expanse.
# areaRadial.angle([angle]) · Source
Equivalent to area.x, except the accessor returns the bending in radians, with 0 at -y (12 o'clock).
# areaRadial.startAngle([angle]) · Source
Equivalent to surface area.x0, except the accessor returns the angle in radians, with 0 at -y (12 o'clock). Note: typically angle is used instead of setting separate showtime and end angles.
# areaRadial.endAngle([angle]) · Source
Equivalent to surface area.x1, except the accessor returns the angle in radians, with 0 at -y (12 o'clock). Note: typically bending is used instead of setting divide beginning and end angles.
# areaRadial.radius([radius]) · Source
Equivalent to area.y, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
# areaRadial.innerRadius([radius]) · Source
Equivalent to expanse.y0, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
# areaRadial.outerRadius([radius]) · Source
Equivalent to area.y1, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
# areaRadial.defined([defined])
Equivalent to area.defined.
# areaRadial.bend([curve]) · Source
Equivalent to surface area.bend. Note that curveMonotoneX or curveMonotoneY are non recommended for radial areas because they assume that the data is monotonic in x or y, which is typically untrue of radial areas.
# areaRadial.context([context])
Equivalent to line.context.
# areaRadial.lineStartAngle() · Source
# areaRadial.lineInnerRadius() · Source
Returns a new radial line generator that has this radial area generator'south electric current defined accessor, curve and context. The line's angle accessor is this area'south start angle accessor, and the line's radius accessor is this area'southward inner radius accessor.
# areaRadial.lineEndAngle() · Source
Returns a new radial line generator that has this radial area generator'southward current defined accessor, curve and context. The line'south angle accessor is this area's end angle accessor, and the line's radius accessor is this expanse's inner radius accessor.
# areaRadial.lineOuterRadius() · Source
Returns a new radial line generator that has this radial surface area generator's current defined accessor, curve and context. The line's angle accessor is this area's start angle accessor, and the line'south radius accessor is this area's outer radius accessor.
Curves
While lines are defined as a sequence of two-dimensional [x, y] points, and areas are similarly defined by a topline and a baseline, there remains the task of transforming this discrete representation into a continuous shape: i.east., how to interpolate between the points. A diversity of curves are provided for this purpose.
Curves are typically not constructed or used directly, instead being passed to line.curve and area.curve. For example:
const line = d3 . line ( d => d . date , d => d . value ) . bend ( d3 . curveCatmullRom . alpha ( 0.5 ) ) ; # d3.curveBasis(context) · Source
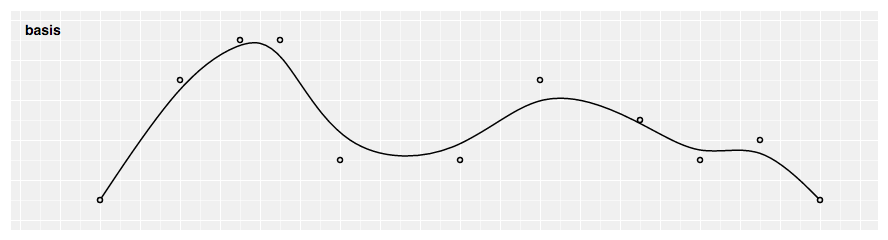
Produces a cubic footing spline using the specified control points. The commencement and last points are triplicated such that the spline starts at the kickoff point and ends at the last point, and is tangent to the line between the showtime and second points, and to the line betwixt the penultimate and last points.
# d3.curveBasisClosed(context) · Source
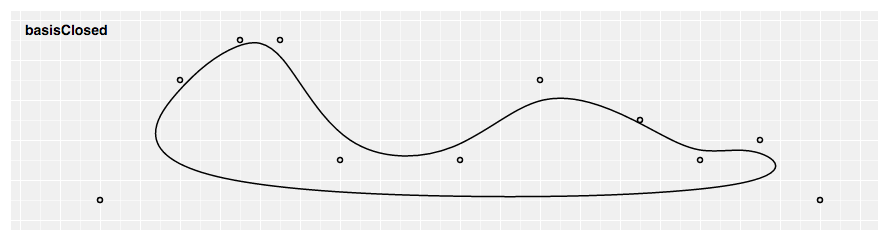
Produces a airtight cubic ground spline using the specified command points. When a line segment ends, the first three control points are repeated, producing a closed loop with C2 continuity.
# d3.curveBasisOpen(context) · Source
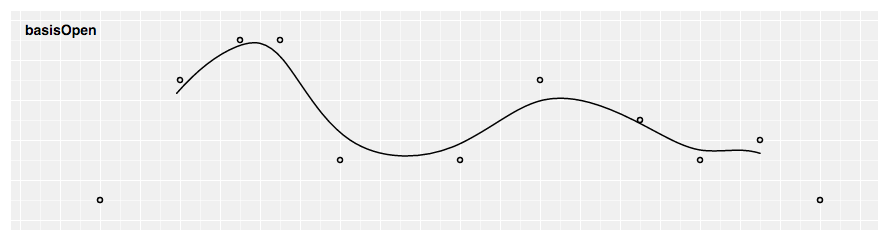
Produces a cubic basis spline using the specified command points. Unlike ground, the first and last points are not repeated, and thus the curve typically does not intersect these points.
# d3.curveBumpX(context) · Source
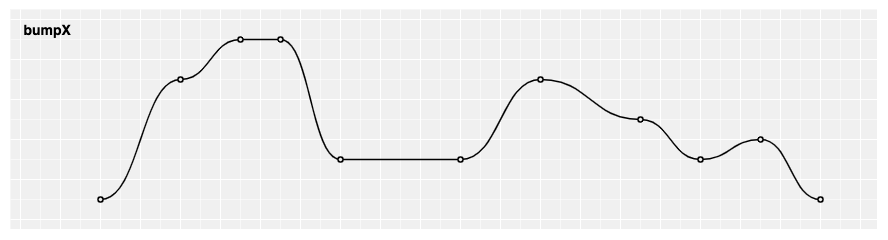
Produces a Bézier curve between each pair of points, with horizontal tangents at each point.
# d3.curveBumpY(context) · Source
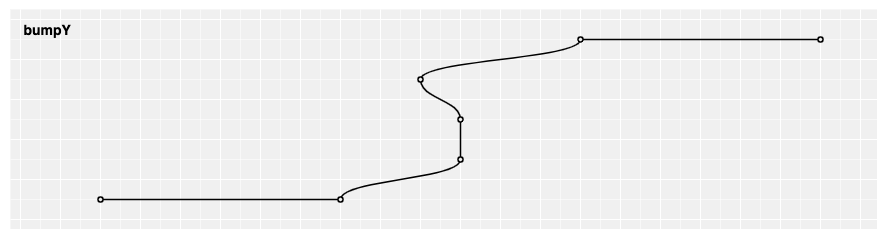
Produces a Bézier curve betwixt each pair of points, with vertical tangents at each point.
# d3.curveBundle(context) · Source
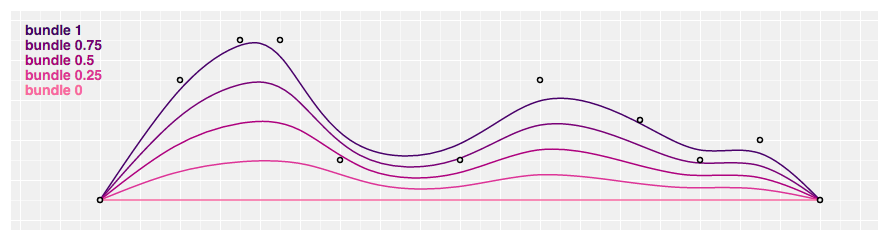
Produces a straightened cubic basis spline using the specified control points, with the spline straightened according to the bend's beta, which defaults to 0.85. This bend is typically used in hierarchical border bundling to disambiguate connections, as proposed by Danny Holten in Hierarchical Edge Bundles: Visualization of Adjacency Relations in Hierarchical Data. This curve does not implement curve.areaStart and curve.areaEnd; information technology is intended to work with d3.line, not d3.area.
# packet.beta(beta) · Source
Returns a bundle curve with the specified beta in the range [0, 1], representing the parcel strength. If beta equals nil, a straight line between the first and concluding point is produced; if beta equals one, a standard footing spline is produced. For example:
const line = d3 . line ( ) . bend ( d3 . curveBundle . beta ( 0.five ) ) ; # d3.curveCardinal(context) · Source
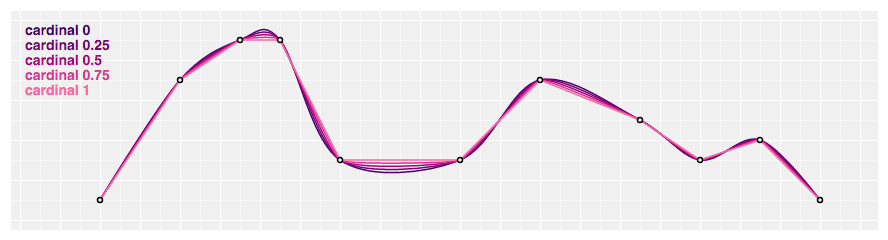
Produces a cubic cardinal spline using the specified command points, with 1-sided differences used for the first and last slice. The default tension is 0.
# d3.curveCardinalClosed(context) · Source

Produces a closed cubic key spline using the specified control points. When a line segment ends, the commencement three control points are repeated, producing a closed loop. The default tension is 0.
# d3.curveCardinalOpen(context) · Source
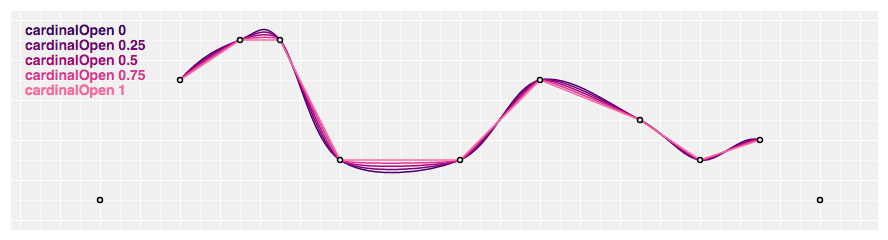
Produces a cubic primal spline using the specified control points. Unlike curveCardinal, i-sided differences are not used for the first and terminal piece, and thus the curve starts at the second point and ends at the penultimate point. The default tension is 0.
# cardinal.tension(tension) · Source
Returns a central bend with the specified tension in the range [0, one]. The tension determines the length of the tangents: a tension of one yields all zero tangents, equivalent to curveLinear; a tension of cypher produces a uniform Catmull–Rom spline. For example:
const line = d3 . line ( ) . bend ( d3 . curveCardinal . tension ( 0.five ) ) ; # d3.curveCatmullRom(context) · Source
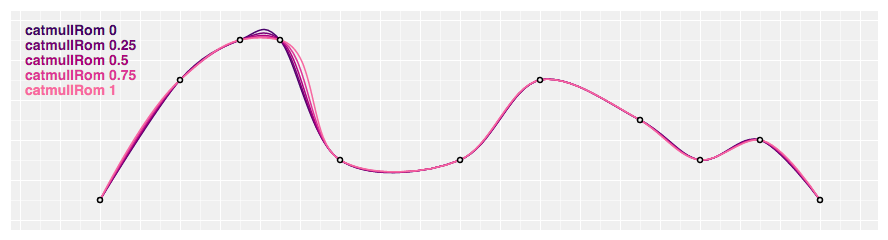
Produces a cubic Catmull–Rom spline using the specified command points and the parameter alpha, which defaults to 0.5, as proposed by Yuksel et al. in On the Parameterization of Catmull–Rom Curves, with 1-sided differences used for the get-go and concluding slice.
# d3.curveCatmullRomClosed(context) · Source
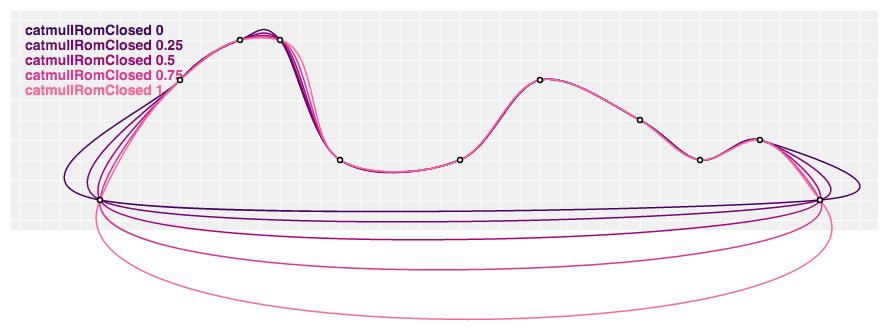
Produces a airtight cubic Catmull–Rom spline using the specified control points and the parameter alpha, which defaults to 0.5, as proposed by Yuksel et al. When a line segment ends, the first three control points are repeated, producing a airtight loop.
# d3.curveCatmullRomOpen(context) · Source
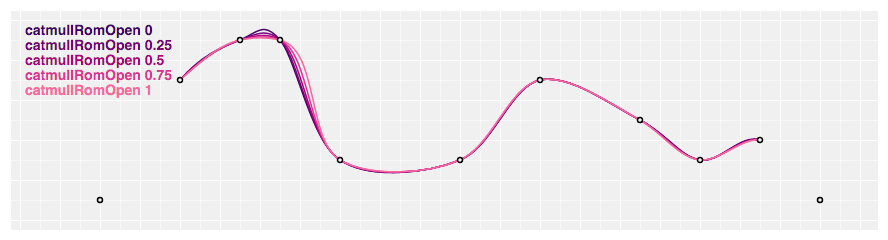
Produces a cubic Catmull–Rom spline using the specified control points and the parameter blastoff, which defaults to 0.5, every bit proposed by Yuksel et al. Unlike curveCatmullRom, one-sided differences are not used for the commencement and last piece, and thus the curve starts at the second point and ends at the penultimate point.
# catmullRom.alpha(alpha) · Source
Returns a cubic Catmull–Rom curve with the specified alpha in the range [0, 1]. If alpha is zero, produces a uniform spline, equivalent to curveCardinal with a tension of nada; if alpha is one, produces a chordal spline; if blastoff is 0.5, produces a centripetal spline. Centripetal splines are recommended to avoid self-intersections and overshoot. For example:
const line = d3 . line ( ) . curve ( d3 . curveCatmullRom . alpha ( 0.five ) ) ; # d3.curveLinear(context) · Source
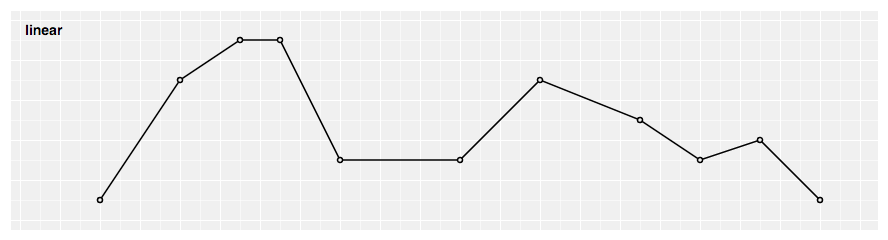
Produces a polyline through the specified points.
# d3.curveLinearClosed(context) · Source
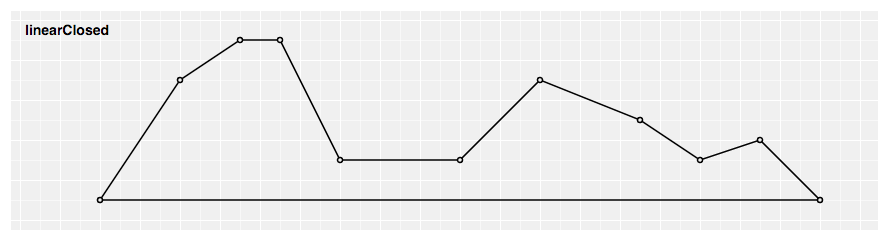
Produces a closed polyline through the specified points past repeating the first signal when the line segment ends.
# d3.curveMonotoneX(context) · Source
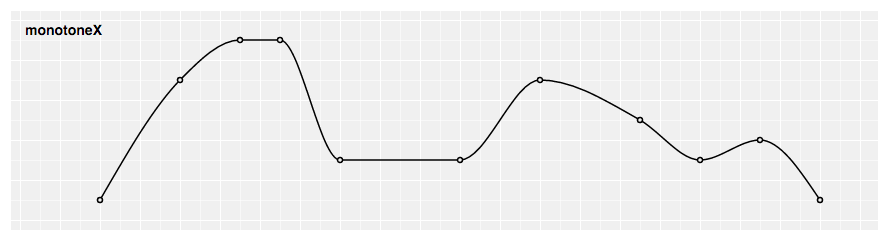
Produces a cubic spline that preserves monotonicity in y, assuming monotonicity in x, equally proposed past Steffen in A uncomplicated method for monotonic interpolation in ane dimension: "a smoothen curve with continuous first-society derivatives that passes through whatsoever given set up of information points without spurious oscillations. Local extrema can occur only at grid points where they are given by the data, but not in between two next grid points."
# d3.curveMonotoneY(context) · Source
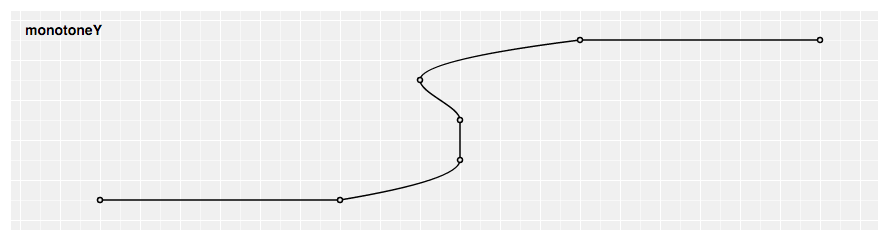
Produces a cubic spline that preserves monotonicity in 10, bold monotonicity in y, as proposed by Steffen in A uncomplicated method for monotonic interpolation in ane dimension: "a smooth curve with continuous first-society derivatives that passes through any given set of information points without spurious oscillations. Local extrema can occur merely at filigree points where they are given past the data, simply not in betwixt two adjacent grid points."
# d3.curveNatural(context) · Source
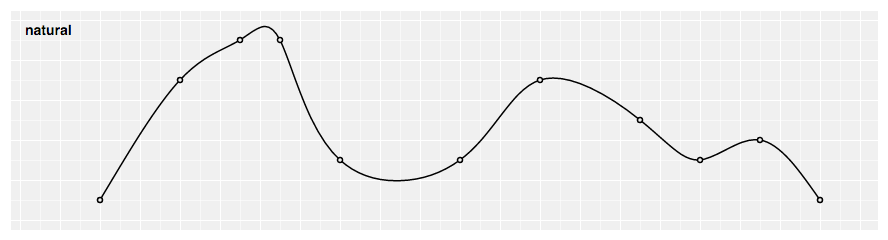
Produces a natural cubic spline with the second derivative of the spline set to zero at the endpoints.
# d3.curveStep(context) · Source
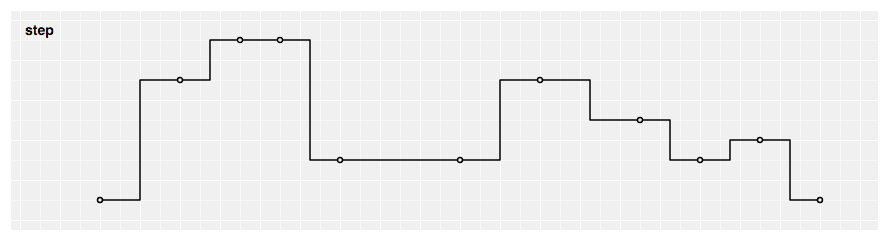
Produces a piecewise constant role (a step function) consisting of alternate horizontal and vertical lines. The y-value changes at the midpoint of each pair of adjacent ten-values.
# d3.curveStepAfter(context) · Source
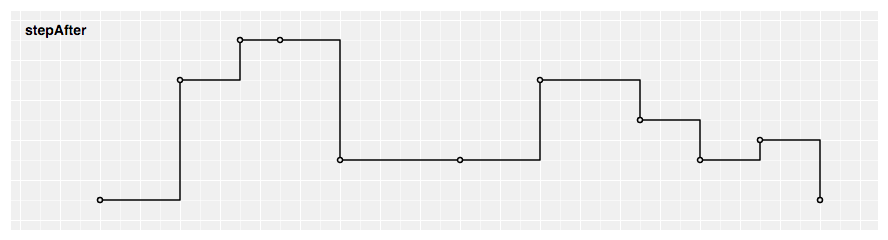
Produces a piecewise constant function (a stride function) consisting of alternating horizontal and vertical lines. The y-value changes subsequently the ten-value.
# d3.curveStepBefore(context) · Source
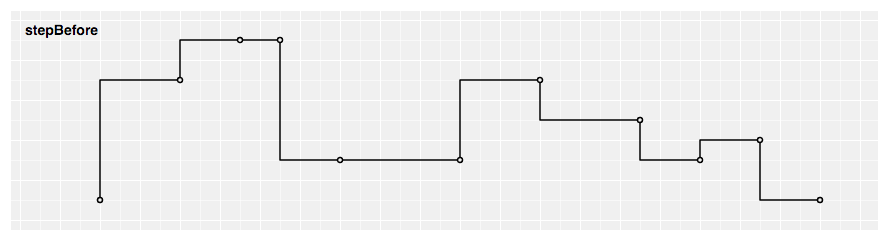
Produces a piecewise constant function (a step function) consisting of alternating horizontal and vertical lines. The y-value changes before the x-value.
Custom Curves
Curves are typically non used directly, instead being passed to line.curve and expanse.curve. However, you lot tin define your own curve implementation should none of the built-in curves satisfy your needs using the post-obit interface. You tin can also use this low-level interface with a congenital-in curve type equally an alternative to the line and area generators.
# curve.areaStart() · Source
Indicates the start of a new area segment. Each area segment consists of exactly two line segments: the topline, followed by the baseline, with the baseline points in contrary order.
# curve.areaEnd() · Source
Indicates the finish of the current area segment.
# bend.lineStart() · Source
Indicates the get-go of a new line segment. Nada or more points will follow.
# bend.lineEnd() · Source
Indicates the end of the current line segment.
# curve.point(x, y) · Source
Indicates a new point in the current line segment with the given ten- and y-values.
Links
The link shape generates a smooth cubic Bézier bend from a source signal to a target point. The tangents of the bend at the starting time and stop are either vertical, horizontal or radial.
# d3.link(curve) · Source
Returns a new link generator using the specified curve. For instance, to visualize links in a tree diagram rooted on the summit edge of the display, you might say:
const link = d3 . link ( d3 . curveBumpY ) . x ( d => d . x ) . y ( d => d . y ) ; # d3.linkVertical() · Source
Autograph for d3.link with d3.curveBumpY; suitable for visualizing links in a tree diagram rooted on the tiptop edge of the brandish. Equivalent to:
const link = d3 . link ( d3 . curveBumpY ) ; # d3.linkHorizontal() · Source
Shorthand for d3.link with d3.curveBumpX; suitable for visualizing links in a tree diagram rooted on the left edge of the brandish. Equivalent to:
const link = d3 . link ( d3 . curveBumpX ) ; # link(arguments…) · Source
Generates a link for the given arguments. The arguments are arbitrary; they are but propagated to the link generator'due south accessor functions along with the this object. For example, with the default settings, an object expected:
link ( { source: [ 100 , 100 ] , target: [ 300 , 300 ] } ) ; # link.source([source]) · Source
If source is specified, sets the source accessor to the specified function and returns this link generator. If source is non specified, returns the current source accessor, which defaults to:
office source ( d ) { return d . source ; } # link.target([target]) · Source
If target is specified, sets the target accessor to the specified function and returns this link generator. If target is not specified, returns the current target accessor, which defaults to:
function target ( d ) { render d . target ; } # link.x([x]) · Source
If x is specified, sets the x-accessor to the specified office or number and returns this link generator. If x is not specified, returns the current 10-accessor, which defaults to:
function x ( d ) { return d [ 0 ] ; } # link.y([y]) · Source
If y is specified, sets the y-accessor to the specified function or number and returns this link generator. If y is non specified, returns the current y-accessor, which defaults to:
function y ( d ) { return d [ 1 ] ; } # link.context([context]) · Source
If context is specified, sets the context and returns this link generator. If context is not specified, returns the current context, which defaults to naught. If the context is non null, and so the generated link is rendered to this context equally a sequence of path method calls. Otherwise, a path data string representing the generated link is returned. See also d3-path.
# d3.linkRadial() · Source
Returns a new link generator with radial tangents. For example, to visualize links in a tree diagram rooted in the center of the display, you lot might say:
const link = d3 . linkRadial ( ) . angle ( d => d . ten ) . radius ( d => d . y ) ; # linkRadial.angle([angle]) · Source
Equivalent to link.10, except the accessor returns the angle in radians, with 0 at -y (12 o'clock).
# linkRadial.radius([radius]) · Source
Equivalent to link.y, except the accessor returns the radius: the distance from the origin ⟨0,0⟩.
Symbols
Symbols provide a categorical shape encoding as is commonly used in scatterplots. Symbols are always centered at ⟨0,0⟩; utilise a transform (see: SVG, Canvas) to move the symbol to a different position.
# d3.symbol([type][, size]) · Source, Examples
Constructs a new symbol generator of the specified type and size. If non specified, type defaults to a circle, and size defaults to 64.
# symbol(arguments…) · Source
Generates a symbol for the given arguments. The arguments are arbitrary; they are simply propagated to the symbol generator's accessor functions along with the this object. For instance, with the default settings, no arguments are needed to produce a circle with area 64 square pixels. If the symbol generator has a context, then the symbol is rendered to this context as a sequence of path method calls and this function returns void. Otherwise, a path data string is returned.
# symbol.blazon([blazon]) · Source
If blazon is specified, sets the symbol type to the specified function or symbol type and returns this symbol generator. If type is a function, the symbol generator'southward arguments and this are passed through. (Meet selection.attr if y'all are using d3-selection.) If type is non specified, returns the current symbol type accessor, which defaults to:
function type ( ) { return circle ; } See symbolsFill and symbolsStroke for built-in symbol types. To implement a custom symbol type, laissez passer an object that implements symbolType.draw.
# symbol.size([size]) · Source
If size is specified, sets the size to the specified office or number and returns this symbol generator. If size is a function, the symbol generator's arguments and this are passed through. (See option.attr if you are using d3-choice.) If size is not specified, returns the current size accessor, which defaults to:
function size ( ) { return 64 ; } Specifying the size as a function is useful for amalgam a scatterplot with a size encoding. If yous wish to scale the symbol to fit a given bounding box, rather than past expanse, try SVG's getBBox.
# symbol.context([context]) · Source
If context is specified, sets the context and returns this symbol generator. If context is not specified, returns the current context, which defaults to nix. If the context is not null, then the generated symbol is rendered to this context every bit a sequence of path method calls. Otherwise, a path data string representing the generated symbol is returned.
# d3.symbolsFill · Source






An array containing a set of symbol types designed for filling: circumvolve, cross, diamond, foursquare, star, triangle, and wye. Useful for amalgam the range of an ordinal scale should you wish to apply a shape encoding for categorical data.
# d3.symbolsStroke · Source
An array containing a set of symbol types designed for stroking: circle, plus, 10, triangle2, asterisk, square2, and diamond2. Useful for amalgam the range of an ordinal calibration should you wish to use a shape encoding for categorical data.
# d3.symbolAsterisk · Source
The asterisk symbol type; intended for stroking.
# d3.symbolCircle · Source
The circle symbol type; intended for either filling or stroking.
# d3.symbolCross · Source
The Greek cross symbol blazon, with arms of equal length; intended for filling.
# d3.symbolDiamond · Source
The rhomb symbol type; intended for filling.
# d3.symbolDiamond2 · Source
The rotated square symbol type; intended for stroking.
# d3.symbolPlus · Source
The plus symbol type; intended for stroking.
# d3.symbolSquare · Source
The square symbol blazon; intended for filling.
# d3.symbolSquare2 · Source
The square2 symbol blazon; intended for stroking.
# d3.symbolStar · Source
The pentagonal star (pentagram) symbol blazon; intended for filling.
# d3.symbolTriangle · Source
The up-pointing triangle symbol type; intended for filling.
# d3.symbolTriangle2 · Source
The upwards-pointing triangle symbol type; intended for stroking.
# d3.symbolWye · Source
The Y-shape symbol type; intended for filling.
# d3.symbolX · Source
The X-shape symbol type; intended for stroking.
# d3.pointRadial(angle, radius) · Source, Examples
Returns the signal [10, y] for the given angle in radians, with 0 at -y (12 o'clock) and positive angles proceeding clockwise, and the given radius.
Custom Symbol Types
Symbol types are typically non used directly, instead being passed to symbol.type. Withal, you can define your own symbol blazon implementation should none of the born types satisfy your needs using the following interface. You tin can also employ this low-level interface with a built-in symbol type every bit an culling to the symbol generator.
# symbolType.draw(context, size)
Renders this symbol type to the specified context with the specified size in foursquare pixels. The context implements the CanvasPathMethods interface. (Annotation that this is a subset of the CanvasRenderingContext2D interface!)
Stacks
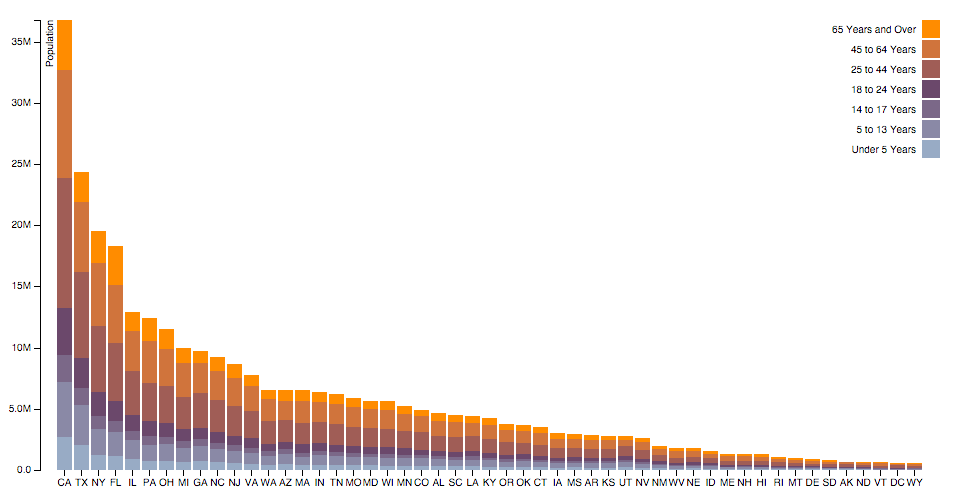
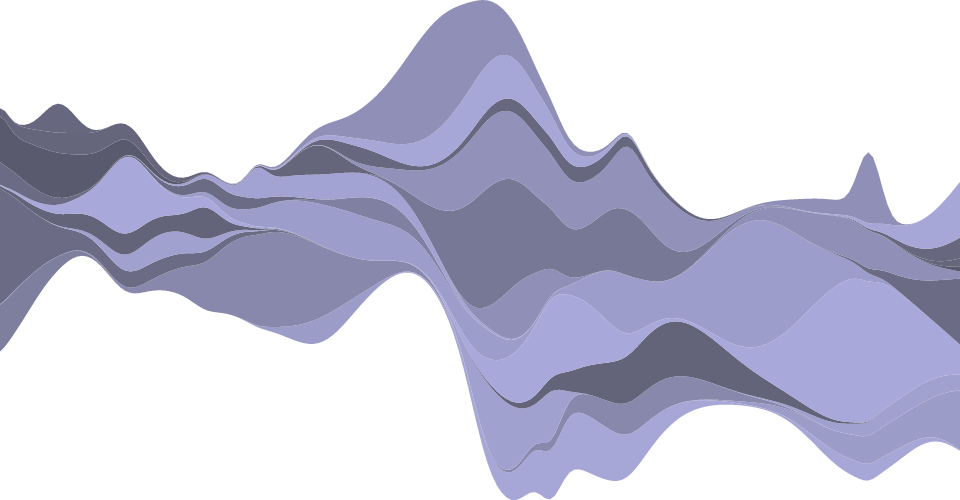
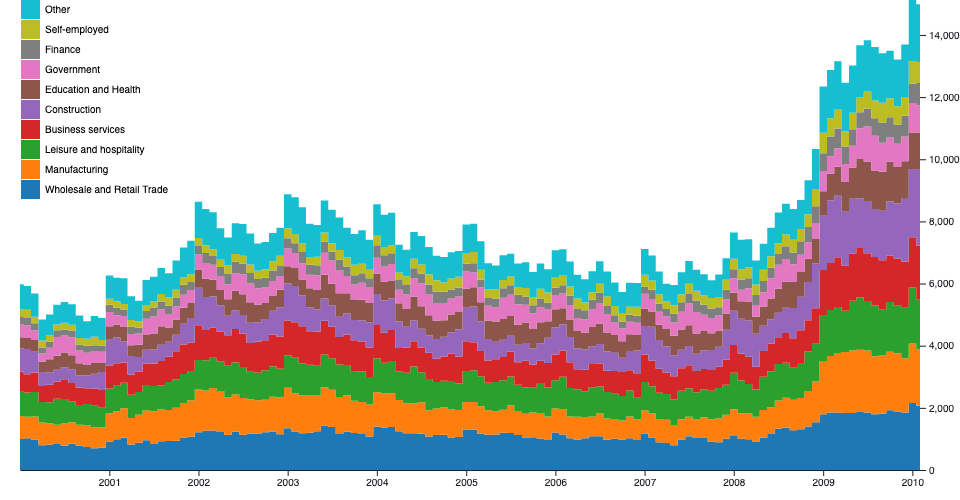
Some shape types can be stacked, placing one shape adjacent to another. For example, a bar chart of monthly sales might be broken down into a multi-series bar nautical chart by product category, stacking bars vertically. This is equivalent to subdividing a bar chart by an ordinal dimension (such as product category) and applying a color encoding.
Stacked charts tin show overall value and per-category value simultaneously; even so, information technology is typically harder to compare beyond categories, equally only the bottom layer of the stack is aligned. Then, chose the stack club advisedly, and consider a streamgraph. (See also grouped charts.)
Like the pie generator, the stack generator does not produce a shape directly. Instead it computes positions which you can then laissez passer to an expanse generator or use directly, say to position bars.
# d3.stack() · Source
Constructs a new stack generator with the default settings.
# stack(data[, arguments…]) · Source
Generates a stack for the given array of data, returning an array representing each series. Whatsoever additional arguments are arbitrary; they are only propagated to accessors along with the this object.
The serial are determined by the keys accessor; each series i in the returned assortment corresponds to the ith key. Each series is an array of points, where each signal j corresponds to the jth chemical element in the input data. Lastly, each bespeak is represented every bit an array [y0, y1] where y0 is the lower value (baseline) and y1 is the upper value (topline); the difference between y0 and y1 corresponds to the computed value for this betoken. The primal for each serial is bachelor equally series.cardinal, and the index as series.index. The input data element for each indicate is bachelor every bit signal.information.
For instance, consider the following table representing monthly sales of fruits:
| Month | Apples | Bananas | Cherries | Dates |
|---|---|---|---|---|
| 1/2015 | 3840 | 1920 | 960 | 400 |
| 2/2015 | 1600 | 1440 | 960 | 400 |
| 3/2015 | 640 | 960 | 640 | 400 |
| 4/2015 | 320 | 480 | 640 | 400 |
This might be represented in JavaScript as an array of objects:
const information = [ { calendar month: new Appointment ( 2015 , 0 , 1 ) , apples: 3840 , bananas: 1920 , cherries: 960 , dates: 400 } , { month: new Engagement ( 2015 , 1 , 1 ) , apples: 1600 , bananas: 1440 , cherries: 960 , dates: 400 } , { month: new Appointment ( 2015 , two , 1 ) , apples: 640 , bananas: 960 , cherries: 640 , dates: 400 } , { month: new Appointment ( 2015 , iii , 1 ) , apples: 320 , bananas: 480 , cherries: 640 , dates: 400 } ] ; To produce a stack for this data:
const stack = d3 . stack ( ) . keys ( [ "apples" , "bananas" , "cherries" , "dates" ] ) . order ( d3 . stackOrderNone ) . outset ( d3 . stackOffsetNone ) ; const series = stack ( data ) ; The resulting array has ane chemical element per serial. Each series has ane point per calendar month, and each point has a lower and upper value defining the baseline and topline:
[ [ [ 0 , 3840 ] , [ 0 , 1600 ] , [ 0 , 640 ] , [ 0 , 320 ] ] , // apples [ [ 3840 , 5760 ] , [ 1600 , 3040 ] , [ 640 , 1600 ] , [ 320 , 800 ] ] , // bananas [ [ 5760 , 6720 ] , [ 3040 , 4000 ] , [ 1600 , 2240 ] , [ 800 , 1440 ] ] , // cherries [ [ 6720 , 7120 ] , [ 4000 , 4400 ] , [ 2240 , 2640 ] , [ 1440 , 1840 ] ] , // dates ] Each series in then typically passed to an area generator to return an expanse chart, or used to construct rectangles for a bar chart.
# stack.keys([keys]) · Source
If keys is specified, sets the keys accessor to the specified function or array and returns this stack generator. If keys is not specified, returns the current keys accessor, which defaults to the empty array. A series (layer) is generated for each key. Keys are typically strings, simply they may be arbitrary values. The serial' key is passed to the value accessor, along with each data bespeak, to compute the bespeak's value.
# stack.value([value]) · Source
If value is specified, sets the value accessor to the specified function or number and returns this stack generator. If value is not specified, returns the electric current value accessor, which defaults to:
function value ( d , key ) { return d [ key ] ; } Thus, by default the stack generator assumes that the input data is an array of objects, with each object exposing named properties with numeric values; see stack for an example.
# stack.gild([guild]) · Source
If order is specified, sets the order accessor to the specified office or assortment and returns this stack generator. If order is not specified, returns the current guild accessor, which defaults to stackOrderNone; this uses the club given by the key accessor. See stack orders for the built-in orders.
If social club is a function, it is passed the generated series assortment and must return an assortment of numeric indexes representing the stack order. For example, the default order is defined equally:
function orderNone ( series ) { permit due north = series . length ; const o = new Array ( n ) ; while ( -- n >= 0 ) o [ n ] = north ; return o ; } The stack social club is computed prior to the get-go; thus, the lower value for all points is zero at the time the order is computed. The alphabetize attribute for each series is besides not set until later the club is computed.
# stack.offset([offset]) · Source
If first is specified, sets the offset accessor to the specified part and returns this stack generator. If offset is not specified, returns the current showtime acccesor, which defaults to stackOffsetNone; this uses a aught baseline. See stack offsets for the built-in offsets.
The showtime function is passed the generated serial array and the gild index array; it is so responsible for updating the lower and upper values in the serial array. For example, the default kickoff is defined as:
function offsetNone ( series , lodge ) { if ( ! ( ( n = series . length ) > 1 ) ) return ; for ( let i = i , s0 , s1 = series [ order [ 0 ] ] , northward , m = s1 . length ; i < n ; ++ i ) { s0 = s1 , s1 = series [ lodge [ i ] ] ; for ( let j = 0 ; j < grand ; ++ j ) { s1 [ j ] [ 1 ] += s1 [ j ] [ 0 ] = s0 [ j ] [ ane ] ; } } } Stack Orders
Stack orders are typically not used directly, but are instead passed to stack.order.
# d3.stackOrderAppearance(series) · Source
Returns a serial society such that the earliest series (according to the maximum value) is at the bottom.
# d3.stackOrderAscending(series) · Source
Returns a series order such that the smallest series (co-ordinate to the sum of values) is at the bottom.
# d3.stackOrderDescending(series) · Source
Returns a serial order such that the largest series (according to the sum of values) is at the lesser.
# d3.stackOrderInsideOut(series) · Source
Returns a series order such that the earliest series (according to the maximum value) are on the inside and the subsequently serial are on the outside. This order is recommended for streamgraphs in conjunction with the wiggle get-go. See Stacked Graphs—Geometry & Aesthetics by Byron & Wattenberg for more information.
# d3.stackOrderNone(series) · Source
Returns the given serial order [0, ane, … n - 1] where n is the number of elements in serial. Thus, the stack order is given by the primal accessor.
# d3.stackOrderReverse(series) · Source
Returns the reverse of the given series order [n - 1, n - ii, … 0] where n is the number of elements in series. Thus, the stack society is given past the contrary of the key accessor.
Stack Offsets
Stack offsets are typically not used direct, merely are instead passed to stack.offset.
# d3.stackOffsetExpand(series, order) · Source
Applies a zero baseline and normalizes the values for each point such that the topline is always one.
# d3.stackOffsetDiverging(serial, order) · Source
Positive values are stacked above zero, negative values are stacked below zero, and zippo values are stacked at nil.
# d3.stackOffsetNone(series, club) · Source
Applies a aught baseline.
# d3.stackOffsetSilhouette(series, order) · Source
Shifts the baseline down such that the center of the streamgraph is ever at nil.
# d3.stackOffsetWiggle(series, social club) · Source
Shifts the baseline then as to minimize the weighted jerk of layers. This offset is recommended for streamgraphs in conjunction with the within-out guild. Meet Stacked Graphs—Geometry & Aesthetics by Bryon & Wattenberg for more information.
Source: https://github.com/d3/d3-shape
0 Response to "lets draw 3d shapes together"
Enregistrer un commentaire